The good news is I made it through seven videos this week, but the bad news is that they were a single series of videos all working through one question and that’s all I managed to get through, AND I didn’t really figure out why the solution works or how the math leading to the solution works. That said, working through the question and watching the videos did help make a few things clearer to me in terms of notation, derivatives/partial derivatives, integrals in general, conceptualizing/visualizing vectors and surfaces in a 3D space, etc. So, all in all, I’m slightly disappointed with how my week went, but it could have been worse.

The section with all seven videos was titled Proof of Stokes’ Theorem. I ended up watching all the videos at least two times, but some of the three or four times. Here are a bunch of screen shots from the seven videos and the notes I took working through the question below:

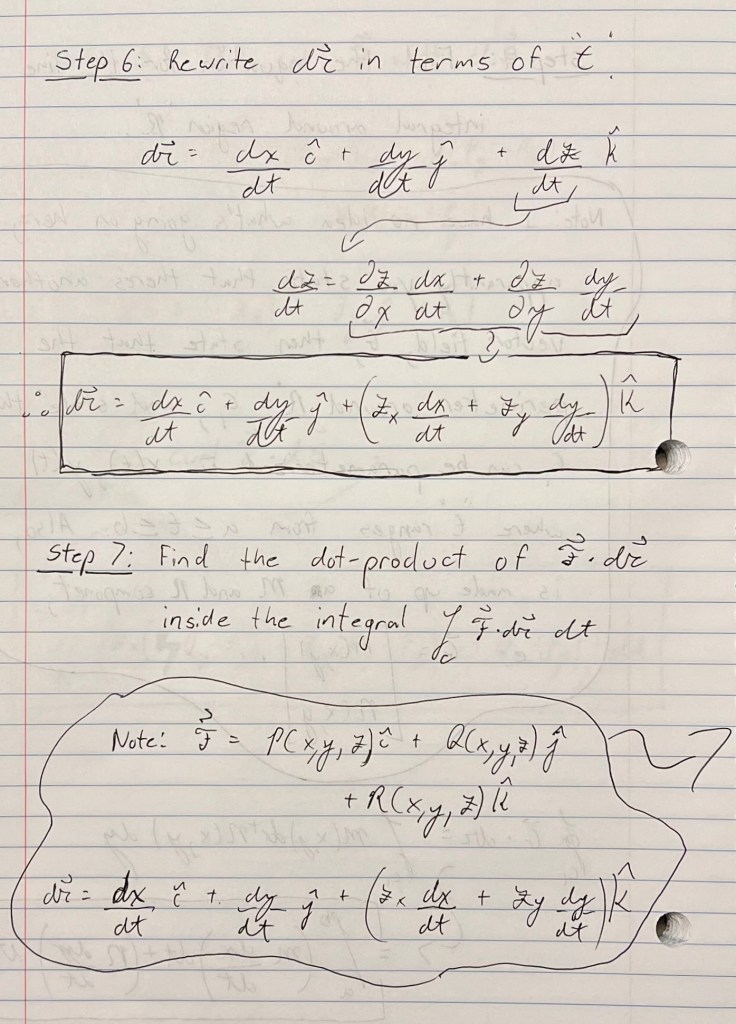
Sal sets up the question by talking about the diagram of the surface in the first screen shot, then stating the “givens”, i.e. the equations for the surface and the vector field, F, and then stating that the line integral of F⋅dr equals the double line integral of the curl of F⋅dS. I still don’t really know what that all means, but I think it means that the value of the sum of the curl of the vectors coming “out” of the perimeter of C is equal to the sum of the curl of the vectors on the entire surface of S. (I’m semi confident that I have the concept correct but am fairly confident I didn’t communicate what I’m trying to express properly.)

The first and second screen shot show Sal working through the double integral of the curl of F where the solution is at the bottom of the second screen shot. For the most part, I was able to follow along and understand how the math worked through these steps and somewhat understand why it worked too. 😮‍💨

The remaining screen shots show Sal working through the other side of the equation, the line integral of F⋅dr. I don’t understand why it works, but Sal begins by stating there’s another vector field G (🤔) and then saying there’s another line integral on the (x, y) plane, C₁, that has the same (x, y) coordinates as C. He then parameterizes the x- and y-coordinates with x = x(t) and y = y(t). He states that C₁ is the line integral of G⋅dr and that G’s components can be set to M and N which is how he rewrites the line integral. He does this so that he can use G.T. shortly.

After that, he works through the line integral of F⋅dr by first finding the dot product of F⋅dr where F is made up of P, Q and R and dr is made up of the partial derivatives of x, y and z. This is where I start to feel lost and not understand what’s going on. I believe that z is a function of x which is a function of t which apparently is why the derivative of z with respect to t requires the chain rule which results in z_x(dx/dt) and z_y(dy/dt).

Sal uses algebra to set all the variables in the line integral of F⋅dr to equal the same thing as the line integral of  G⋅dr which then (apparently) means he can use Green’s Theorem on the line integral of C because it equals  C₁. (I have no clue why that works or how it’s true…) He wraps up the question by using algebra on all the variables in the integrand which ends up turning into the exact same solution as the double integral of the curl of F.

… And I understood about half of that entire thing. 😒

It’s frustrating that I don’t really know what’s going on, BUT I know I’m getting closer and am confident I’ll understand it at some point, but I’m guessing probably not until a few subjects down the road. Regardless, I’m officially eight videos away from being able to start the unit test for Green’s, Stokes’, and the Divergence Theorems (400/600 M.P.), so I’m fairly confident I should be able to get to it this coming week. The eight videos are split between two sections where the first one that talks about three different types of regions and the second section goes through a proof for the divergence theorem. Fingers crossed that I can at least get through all the videos this week and maybe even get started on the unit test. 🤞🏼