It was another mediocre week for me on KA. I “finished” the final exercise from the Divergence Theorem section, but I knew all four solutions to the questions from having seen them all before, so I didn’t have to actually apply myself to understand the questions and finish the exercise. I read all three articles from the following section, Divergence Theorem (Articles), which helped me understand what divergence theorem is all about and helped a little with my understanding of how to apply the divergence theorem, but I still don’t have a great understanding of why the math works for the divergence theorem. This week I also spent ~2 hours watching the end of the Professor Leonard video I was talking about last week, and then also watching his video on Green’s Theorem. I didn’t make any notes on those vids, but they definitely helped me get a better understanding of what’s going on with all of this. So, all in all, it wasn’t a bad week but, as usual, it could have been better.

I once again don’t have much time this week to write this post and I STILL am not feeling great (although, fingers crossed 🤞🏼, I think I may be starting to feel better) so, like last week, I’m not going to spend much time explaining my notes. Here are a handful of screen shots from the three articles I read that go over the notation used in divergence theorem and the benefits of using, and reasoning behind, the divergence theorem:

These screen shots above don’t exactly make it clear but, as you can see from my notes, the connection I made this week is that the divergence theorem is the same as Green’s Theorem and Stokes’ Theorem in that all the theorems relate what’s going on INSIDE of a closed region or surface to the divergence or curl on the OUTSIDE of the perimeter or surface. So, whether you’re looking at curl or divergence, all of these theorems just state that the sum of the vectors on the inside of the shape will always equal the sum of the vectors on the perimeter or surface of the shape. Like I said, I still don’t know why the math works, but knowing that these theorems relate to each other in this way seems to make them easier to grasp.

Again, I’m not going to go through my notes in detail, but here are two example questions I worked through from the third article:

Example 1

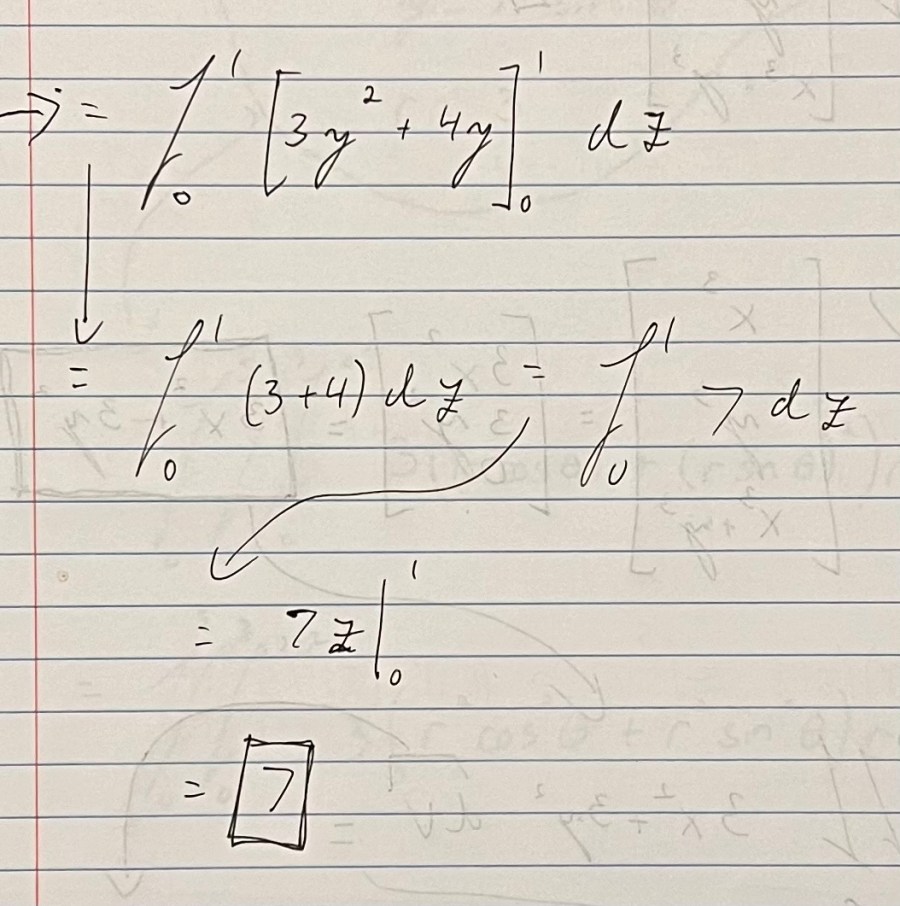
Example 2

It seems like these examples are intentionally very straightforward and simple questions on divergence theorem to make it easy to grasp the general idea of what’s going on and how to do the math, so overall I didn’t find these questions too hard to work through. Understanding why the math works, however, is a different store…

Finally, here are the two Professor Leonard videos I watched this week:

And that’s going to do it for this week’s post. There’s no way I’m going to get through the remaining 15 videos by the end of this week which was my goal, but that’s ok. I’ve officially finished all the articles and exercises from Green’s, Stokes’, and the Divergence Theorems (400/600 M.P.) and I just realized that means I’ve finished all the articles and exercises from ALL of Multivariable Calculus. 😳 I’m getting SO close to finishing this whole thing off. As always, I’m praying to the math gods that I can make some decent progress this upcoming week so I can get there soon. 🙏🏼 🙏🏼 🙏🏼