I’m happy to say that it was a fairly productive week for me back on KA! I made it through eight videos and had a somewhat decent grasp on everything that was covered. It was nice to be back on KA and felt like a throwback. 😂 I’m also glad to say that I’m confident Dr. TB’s Linear Algebra playlist helped me understand what Sal was talking about in the videos this week. To be fair, there were definitely some things that went over my head, but I felt much less out of my depth this week than I did a few months ago when I switched from KA to DR. TB’s videos. Anyways, I’m officially into the second unit of KA’s Linear Algebra course, Matrix Transformations, which I’m pumped about. I still have a long way to go before finishing off this course, but I’m making progress and, more importantly, actually feel like I’m understanding some of what’s been talked about. 😮‍💨

Here are screenshots and pictures of my notes from the eight videos I watched this week:

Video 1 – Proof: Any Subspace Basis has Same Number of Elements

I was kind of annoyed by this video. There’s a very good chance that I missed the point of what Sal was try to explain, but as you can see in my notes, it seemed like all he was saying was that if you have some basis with n dimensions denoted with n basis vectors, you can’t have another basis that has less than n dimensions that spans the OG basis. The video went through the algebra for this and was 21 minutes long. If I’m correct about what the video was talking about, it felt like it took waaay too long to explain that concept.

(That’s why I think I may have missed the point of this video, because it took such a long time to explain what seemed like a pretty straightforward concept. 🤔)

Video 2 – Dimension of the Null Space or Nullity 

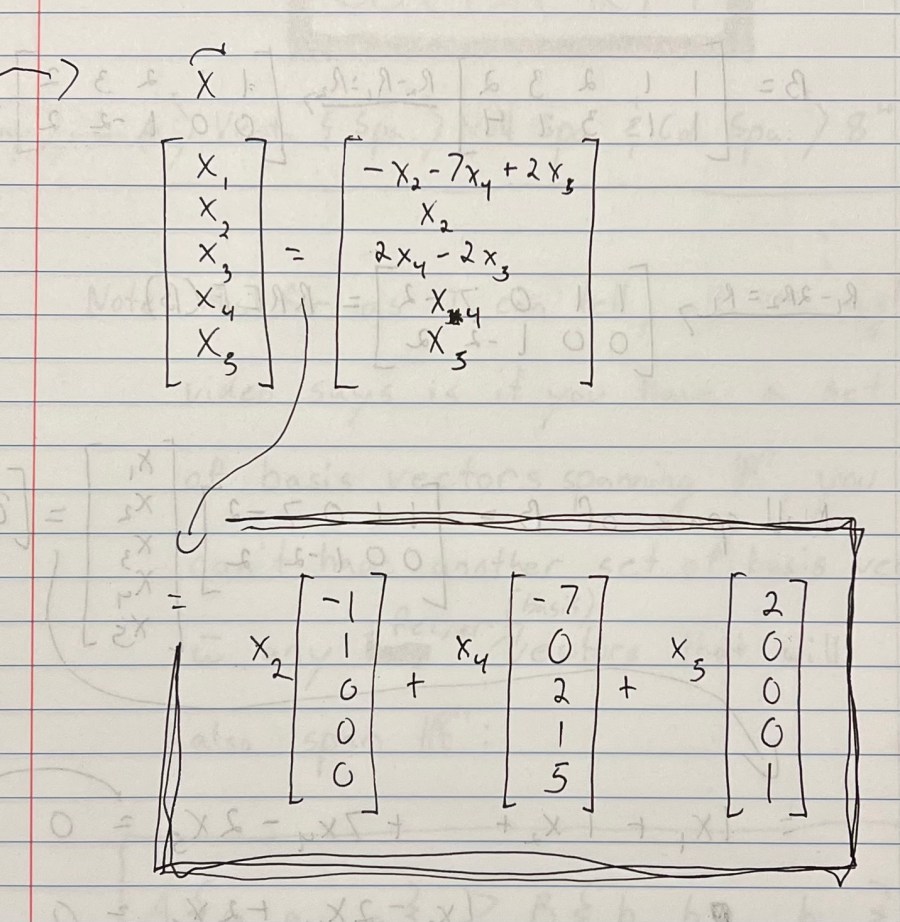
I kind of forget what was going on in this video. I made a note, however, that I worked through the math BEFORE watching Sal work through it and got it correct. ☺️ I think what he was getting at was that to figure out the null space of a matrix transformation you turn a the matrix into its REF form and figure out how many non-pivot columns there are. However many non-pivot columns there are, that’s the dimension of the null space. (I think.)

Video 3 – Dimension of the Column Space or Rank

This video is related to the previous one but instead of finding the null space, Sal found the column space. Whereas the dimension of null space was equal to the number of columns that were non-pivot columns in an REF matrix, the dimension column space is equal to the number of pivot columns. (Maybe…)

Video 4 – Showing Relation Between Basis Columns and Pivot Columns

This video continued on directly from the previous one. In my notebook I wrote that Sal explains the proof that if you REF a matrix, the pivot columns will denote the column space.

(Now that I’m reading through my notes and looking at the screenshot above, I may have this backwards. 🫤)

Video 5 – Showing that the Candidate Basis Does Span C(A)

Ok, so come to think of it, I actually don’t understand what’s going on… I was planning to rewrite my notes from this video, but I don’t know what’s happening so I don’t know how to rewrite them. Here’s a picture from my notebook of what I was planning to rewrite:

I’m pretty sure this is all just proving that the column space for a matrix is made up of the pivot columns and its dimension is equal to the number of pivot columns, but I’m not sure.

Video 6 – A More Formal Understanding of Functions

I think the notes I wrote out do a pretty good job explaining what this video was talking about, so I won’t elaborate. One thing I will say though is that this was the first video from the second unit AND I had to start a new notebook at the exact same time. Very satisfying, and obviously worth mentioning. 😊

Video 7 – Vector Transformations

This video was all about the names and definitions for the different types of notations used in matrix transformations. I also wrote down that “a transformation is a function operating on vectors often denoted with T, for example T(x, y)”.

Video 8 – Linear Transformations

In this video Sal explained what a linear transformation is and the requirements a transformation must meet to be considered a linear transformation. The two requirements are 1) If you add two vectors and then multiply them by a transformation the solution must be equal when applying the transformation to each vector individually and then adding their individual solutions, and 2) if you scale a vector and then apply a transformation, that must equal the same thing as doing a transformation to the vector and then scaling it by the same factor. As you can see at the end of my written notes, generally transformations will be linear when applied to vectors whose elements are all raised to the power of 1.

And that was it for this week. Not too bad, although I’m clearly still a bit confused by the column and null space of a matrix, BUT I do think I’m getting closer to figuring it all out. There are two exercises and eight remaining videos in this first section of Matrix Transformations, all of which I’m hoping to get through this coming week. Based on how fast (read: slow) my progress has been lately, it might not happen. I have a lot more confidence heading into it having gone the Dr. TB’s playlist though! Plus, I’m thinking the videos might not be too difficult given that they’re at the start of the unit. But in any case, I’m just happy to be back on track to getting through KA at some point in my lifetime. Hopefully sooner than later! 🤞🏼